
There is something I have been wanting to apply to LEGO for a long time but that for some reason I could not find enough time to do: a regression analysis.
For those of you that have never heard of have already forgotten what a linear regression is, I will try to quickly summarize the most important aspects. Basically, by running a regression analysis we can determine the relationship between several different independent variables and how they affect one particular dependent variable, therefore allowing us to determine exactly what causes that independent variable to change. Even more, once we have performed a regression analyses we end up with a linear equation that can help us predict the future value of the independent variable by changing one or several of the dependent, with a margin of error depending on the quality of the regression. I know that some will understand this better once we get into the actual UCS numbers.
What I did in this particular case is select a popular theme that had a manageable amount of retired sets so that I would not need to spend several days collecting data, and the UCS seemed to be the most useful choice. For my independent variable I selected Change Over Retail, and the dependent variables that would help me determine it ended up being the following:
- Price Per Piece
- Price Per Gram
- Piece Count
- MSRP
- Total Number of Sets Sold in the Past 12 Months
- Approximate Numbers of Years Retired
There are several other variables that more than likely have an impact in how much a set increases in value over its retail price, like amount of exclusive pieces and actual sales numbers from its entire production run, but they are very hard or even impossible to quantify. The ones I selected are probably the most important of the ones we easily have access to.
After selecting my variables, I went ahead and made a table in Excel for every single one of the UCS already retired sets and collected data for the variables above for each. Here is what it ended up looking like:
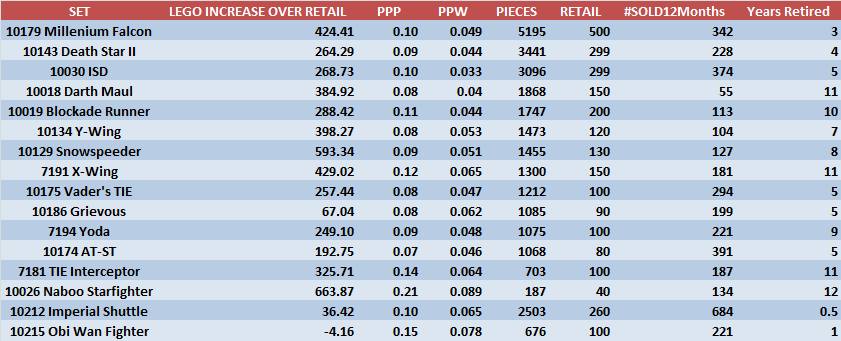
You see that there is a lot of information in the table above that will help us with our current analysis. After collecting the data, I proceeded to run the regression analysis using Excel. The following is the regression output.
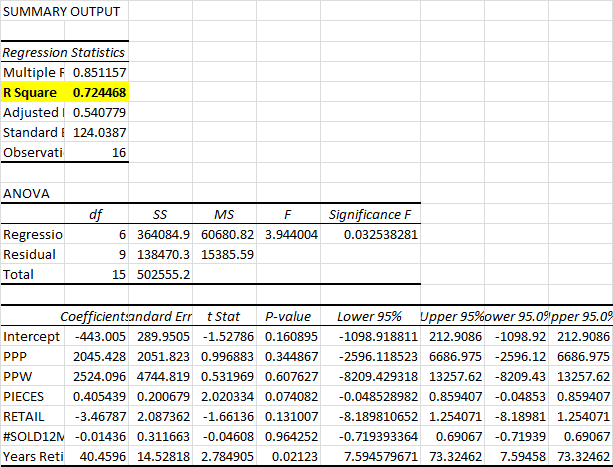
There are a lot of numbers in the table above, but this is not supposed to be an in depth stats class, so I highlighted one of the most important numbers. The highlighted R Square figure is the number that lets us know how much of the variation in a set's % Change over retail is explained by the variables listed below (PPG,PPP, MSRP, etc). In this particular case, we got an R Square of 0.72, or 72%, meaning that we can explain 72% of the movements in Change over retail by using this model. Why can't we explain more than that? well, it all comes down to not having more sets to include (only 16 have been retired) and the fact that we do not have all the variables that have an effect on a set's change over retail. Still, 72% is a pretty respectable number all things considered.
Now the boring part is out of the way, let's put to use what we found out and see how well our model matches up to the actual Change over retail of each set. This is done by using the following equation gathered from the above output:
Predicted % Change Over Retail =-443 + 2045*(PPP) + 2524*(PPW) + 0.41*(#Pieces) - 3.47*(MSRP) - 0.01*(SetsSold12Mo) + 40.46*(#YearsRetired)
You basically substitute each set's information for each variable in the formula above. For example, the 10179 predicted change over retail would be:
Predicted % Change Over Retail =-443 + 2045*(0.1) + 2524*(0.049) + 0.41*(5195) - 3.47*(500) - 0.01*(342) + 40.46*(3)
Predicted % Change Over Retail = 374.01% Actual Change Over Retail = 424.41%
As said before, there is a margin of error tied to the fact that not all of the variables are accounted for, but for basic estimations this model will give you some decently accurate results most of the time. Keep in mind that some special cases will be farther apart from the actual results, while some will be extremely close.
I then went ahead and applied the formula for every single set and compared the predicted values to the actual values just like we did with 10179 above, here is what it looks like both in table and graph form:
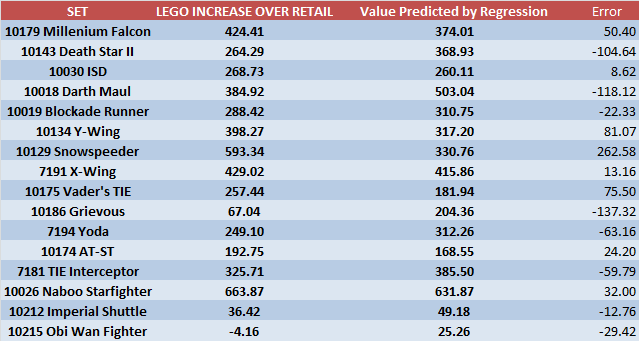
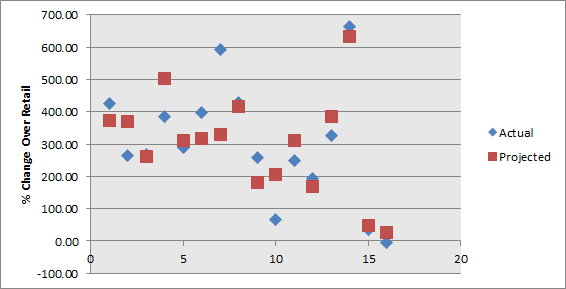
You can see that some of the results are pretty accurate, a couple are very far away (especially Grievous and the Speeder), and most are somewhat close. With more observations (sets) and with at least some of the missing variables our results would be a lot more accurate, but I think this at least provides you with a rough projection of where a set might be once retired for X amount of years.
So, we have been using this model to see how well it predicted performance of sets that have already been retired, but the real usefulness of it is going to be predicting the % change over retail of sets that are currently being produced and sold at retail OR those sets that have already been retired but you want to know where they will be in a couple more years. I will do one example so you can see this better:
10225 R2-D2 Predicted Change Over Retail in 3 Years (Assume retirement this year)
% Change = -443 + 2045*(0.08) + 2524*(0.069) + 0.41*(2127) - 3.47*(180) - 0.01*(676) + 40.46*(3)
Predicted % Change = 244.61%
So, according to the formula, this model should be worth around $ 620 once it has been retired for a period of three years, equivalent to a 244.61% change over retail.
I included this predictor in the Excel file you will find below, but there are some things I want you to keep in mind while using it:
- Projections are not perfect, just estimates
- The model assumes past performance trends will maintain, since that is all the data we have, but as we all know the LEGO investment environment has changed
- Do not try to project values beyond 12 years, since that is the farthest data point we have and will make your results more inaccurate.
- Have Fun!!
Thanks for Reading!
-

Regression - Predictor.xlsx (17.56KB): 128





Recommended Comments
There are no comments to display.
Join the conversation
You can post now and register later. If you have an account, sign in now to post with your account.
Note: Your post will require moderator approval before it will be visible.